beepbeep
다음 순열(Next Permutation) 구하기 본문
알고리즘 문제를 풀던 중 다음 순열을 구하는 문제가 나왔습니다. 그래서 관련 내용을 공부한 후, 정리해 보았습니다.
다음 순열(Next Permutation)이란?
일단 다음 순열을 구하기 위해선, 다음 순열이 무엇인지부터 살펴보아야 할 것 같습니다.
1, 2, 3
예를 들어서 1부터 3까지 적힌 카드가 주어지고, 이 카드를 나열해서 백의 자리 수를 만들어본다고 하면
세 카드를 이용해서 만들어낼 수 있는 백의 자리 수 중 가장 작은 숫자는 123입니다.
그 다음으로 작은 숫자는 132이고, 또 그 다음번 숫자는 213이 됩니다.
만들어낼 수 있는 백의 자리 수를 전부 찾아 오름차순으로 나열하면 다음과 같습니다.
123
132
213
231
312
321
만들어진 백의 자리 숫자를 다시 세 개의 카드로 분리해내면 다음과 정렬된 순열을 얻을 수 있습니다.
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
이 때, [1, 2, 3] 다음에는 [1, 3, 2]가 오고, [2, 1, 3] 다음에는 [2, 3, 1]이 옵니다.
이런 식으로 순열을 정렬해서 나열한다고 할 때, 어떤 순열 다음에 오는 순열을 간단하게 다음 순열이라고 합니다.
다음 순열 구하기
다음과 같은 순열이 주어졌습니다. 이 순열의 다음 순열은 무엇일까요?
[1, 2, 4, 3]
아마 무의식적으로 다음 순열이 떠오르셨을 것 같습니다. 바로 [1, 3, 2, 4] 입니다.
이때 어떻게 다음 순열을 떠올리게 되었는지 천천히 되짚어보면, 다음 순열을 구하는 코드도 작성할 수 있습니다!
우선, 주어진 순열의 끝에서부터 숫자를 하나씩 확인합니다. 이 때, 숫자가 작아지는 지점을 만나면 멈추고 해당 지점을 기억합니다.
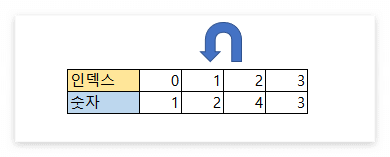
인덱스 2에서 인덱스 1로 넘어갈 때, 숫자가 4에서 2로 작아지는 것을 확인할 수 있습니다.
그러면 해당 지점을 기준으로 배열을 왼쪽 부분과, 오른쪽 부분으로 나눕니다.

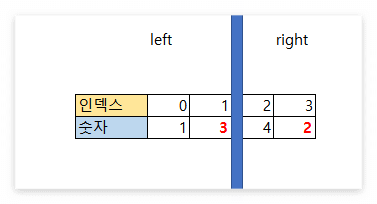
왼쪽 부분에서, 가장 오른쪽에 위치한 숫자를 찾습니다. 이 숫자를 a라고 하겠습니다.
오른쪽 부분에 있는 숫자 중에서, a보다 큰 숫자를 찾고, 그 숫자들 중에서 가장 작은 숫자를 찾습니다. 이 숫자를 b라고 할게요.
위 표에서 a는 2, b는 3이 되겠습니다. 이제 a와 b 두 숫자의 위치를 바꿔줍니다.
복습도 하고 성능도 개선할 겸 해서 다른 풀이를 참고하면서 코드를 고치다가 알게되었는데
"오른쪽 부분"의 숫자가 항상 내림차순으로 정렬되어 있었습니다.
이 점을 이용하면 숫자 b를 더 빨리 찾을 수 있을 것 같아요.
즉 기존에는 조건을 여러 개 사용해서 숫자 b를 찾았다면
이제는 내림차순으로 정렬된 점을 이용해, 배열의 끝에서부터 a의 앞까지 탐색하면서, a보다 큰 숫자가 나오면 반복을 멈추고 그 숫자를 b에 대입하는 방식으로 고쳤습니다.
숫자의 위치를 바꾸었으면 오른쪽 부분에 있는 모든 숫자를 오름차순으로 정렬해줍니다.
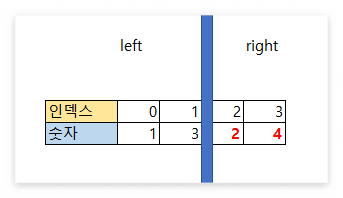
그러면 다음 순열인 [1, 3, 2, 4]를 얻을 수 있습니다!
위의 과정 그대로 코드로 작성하면, 다음 순열을 구할 수 있습니다.
아래 코드는 제가 공부하면서 배운 내용을 참고해 작성한 다음 순열을 구하는 코드입니다.
// n+1과 n을 비교하기 위해서 길이에서 -2를 했습니다.
int n = nums.length-2;
while(n >= 0 && nums[n]>=nums[n+1]){
n--;
}
// n이 0보다 작은 경우, 마지막 순열에 해당합니다.
// 이 경우 더 이상의 작업이 필요하지 않을 수도 있고,
// 오름차순으로 정렬해 첫 번째 순열로 만들어야 할 수도 있습니다.
if(n>=0){
int m = nums.length -1;
while(nums[n]>=nums[m]) m--;
int swap = nums[n];
nums[n] = nums[m];
nums[m] = swap;
}
// 오름차순 정렬1
// for(int i=n+1; i<nums.length; i++){
// for(int j=i+1; j<nums.length; j++){
// int sort = nums[i];
// nums[i] = nums[j];
// nums[j] = sort;
// }
// }
// 오름차순 정렬2
int i = n+1;
int j = nums.length-1;
while(i<j){
int sort = nums[i];
nums[i] = nums[j];
nums[j] = sort;
i++;
j--;
}'코딩테스트 연습 > 투 포인터, 그리디, DP' 카테고리의 다른 글
| LeetCode 11번 - Container With Most Water (0) | 2023.02.24 |
|---|---|
| LeetCode 202번 - Happy Number (0) | 2023.02.02 |
| LeetCode 121번 - Best Time to Buy and Sell Stock (0) | 2023.01.28 |

