beepbeep
LeetCode 11번 - Container With Most Water 본문
문제
int 자료형 배열이 주어집니다.
배열에서 두 값을 꺼내서 용기를 만들어보려고 합니다. 이 때 두 값은 용기의 양쪽 높이가 되고, 두 값의 인덱스의 차이는 너비가 됩니다.
예를 들어 [1, 3, 7, 4, 5] 라는 배열이 있고 이 배열에서 3과 5를 꺼냈을 때, 상자의 한쪽 높이는 3, 반대쪽 높이는 5가 되고 상자의 너비는 두 값의 인덱스의 차이인 3(4 - 1)이 됩니다.
이렇게 만든 2차원 모양의 용기에 물을 담으려고 합니다.
가장 많은 양의 물을 담을 수 있는 용기를 찾아서, 그 용기에 담을 수 있는 물의 양을 계산하세요.
살펴보기
생각을 정리하다보니 내용이 길어졌는데... 요약하면 다음과 같다.
문제 핵심)
1. 인덱스를 가운데로 옮길 때마다 용기의 너비가 줄어든다. 즉, 담을 수 있는 물의 양이 줄어들 수 있다.
2. 용기에 담을 수 있는 물의 양은 너비 * 양쪽 높이 중 작은 쪽의 높이 이다.
풀이 방식)
i) 두 개의 포인터를 배열의 양쪽 끝에 위치시킨다.
ii) 용기의 크기를 계산한다.
iii) 두 포인터 중, 가리키는 값(높이)이 더 작은 쪽의 포인터를 가운데로 한 칸 이동시킨 후 다시 크기를 계산한다.
iiii) 두 포인터가 마주칠 때까지 iii를 반복한다.
일단 가장 먼저 생각난 방법은 이중반복문을 이용하는 방법이었다. 이중반복문을 통해 모든 경우의 수를 찾고, 그 중 가장 큰 값을 찾아 반환하는 단순한 방법이었다. 혹시나 하는 마음에 코드를 적고 제출해봤는데 역시나.. 시간 제한에 걸렸다.
그래서 두 포인터를 사용해 풀어보기로 했다.
포인터 하나는 배열의 첫 부분( arr[0] )부터, 다른 하나는 배열의 끝 부분( arr[length() -1] )부터 시작해서, 두 포인터를 가운데로 이동시키면서 문제를 풀어보았다.
용기를 계산할 때에는 다음의 내용을 꼭 기억해야 한다..
i) 포인터를 가운데쪽으로 옮길 때마다 용기의 너비가 줄어든다. 즉, 담을 수 있는 물의 양이 점차 줄어들게 된다.
ii) 용기에 담을 수 있는 물의 양은 너비 * 양쪽 높이 중 작은 쪽의 높이 이다.
이 두 가지를 적어놓고 해답을 찾아보았다.
1. 두 포인터를 동시에 이동시키기
일단 이 방법은 100% 안될 것이다..

예를 들어 위 사진과 같은 배열이 있을 때, 가장 큰 면적은 양 높이가 [11, 7]일때 얻을 수 있다.
그러나 두 포인터를 동시에 이동시키는 경우..
[10, 7]
[11, 3]
[3, 3]
이 세 가지 경우만 얻을 수 있다. 즉 원하는 값을 찾을 수 없다.
2. 두 포인터 중 포인터가 가리키는 값(=높이)이 작은 쪽만 가운데로 이동시키기
ii) 용기에 담을 수 있는 물의 양은 너비 * 양쪽 높이 중 작은 쪽의 높이 이다.
두 포인터를 가운데로 이동시키되, 두 포인터 중 높이가 작은 쪽만 가운데로 이동시켜야 한다.
예를 들어 [5, 112, 5, 3, 11, 6]의 배열이 주어졌다고 가정해보았다.

이 배열에서 만들어낼 수 있는 가장 큰 용기는 높이가 각각 12, 11일 때이다.
이제 두 개의 포인터 i와 j를 각각 양쪽 끝에 배치시킨 후 이동시켜보았다.
일단 현재 i=0, j=5이며 두 값을 이용해 만든 용기에 담을 수 있는 물의 최대량은 (5-0)*6=30 이다.
이제 높이가 작은 쪽의 포인터를 이동시켜보았다... i가 1칸 오른쪽으로 이동하게 된다.
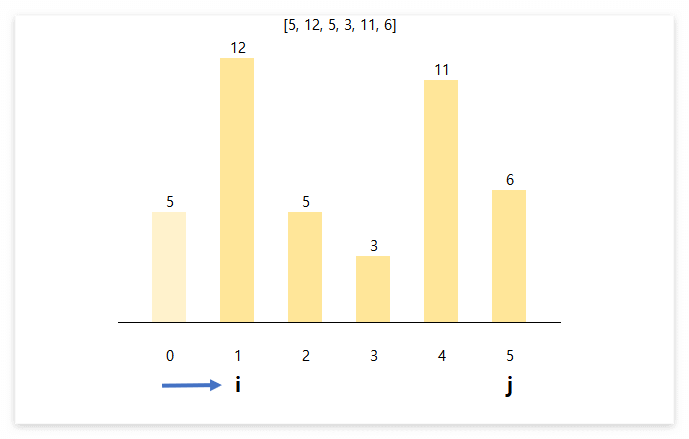
i=1, j=5이며 한 쪽 높이가 12로 엄청 커졌지만, 작은 쪽은 6밖에 안된다.
따라서 담을 수 있는 물의 최대량은 (5-1)*6=24 이다..
다시 높이가 작은 쪽, j를 왼쪽으로 한 칸 이동시켜보았다.

i=1, j=5, 양쪽 높이가 12, 11로 바뀌었다.
이 중 작은 쪽의 높이를 이용해서 용기를 계산해야 하므로 물의 최대량은 (4-1)*11=33 이다.
이런 방식으로, 높이가 작은 쪽의 포인터를 가운데를 향해 한 칸씩 이동시키면서 담을 수 있는 물의 최대량을 찾으면 문제를 해결할 수 있다.
번외. 만약 양쪽 끝 중 한 쪽은 고정하고, 다른 한 쪽의 인덱스만 이동시킨다면?
용기에 담을 수 있는 물의 양은 너비와, 작은 쪽의 높이로 결정된다..
따라서 만약 한 쪽 높이를 고정시킨다면, 고정시킨 높이보다 큰 높이의 물을 담을 수 있는 용기를 얻을 수 없다.

예를 들어 위와 같은 배열이 주어졌을 때, 만약 오른쪽을 고정시키고 왼쪽만 이동한다면?
[15, 7], [12, 7], [8, 7], [3, 7], [15, 7]
위의 5개의 조합을 얻을 수 있다.
[15, 7], [12, 7], [8, 7], [3, 7], [15, 7]
왼쪽 높이가 고정시킨 높이인 7보다 크면 용기에 담을 수 있는 물의 높이는 7이 되고,
[15, 7], [12, 7], [8, 7], [3, 7], [15, 7]
왼쪽 높이가 고정시킨 높이인 7보다 작으면 용기에 담을 수 있는 물의 높이는 7보다 작아지게 된다.
즉 높이가 7보다 큰 용기를 찾을 수 없게 된다... 따라서 이 방법으로는 원하는 값을 찾을 수 없다.
풀어보기
int i = 0;
int j = height.length - 1;
int area = 0;
while(i<j){
int temp = (j-i) * Math.min(height[i],height[j]);
if(temp > area) area = temp;
if(height[i]>height[j]){
j--;
} else {
i++;
}
}
return area;변수 i는 배열의 첫 부분에, j는 배열의 끝 부분에 배치한 후 두 변수를 배열의 가운데로 이동시키면서 용기에 담을 수 있는 물의 양을 계산했다.
계산 결과는 변수 area를 이용해 저장했다.
만약 계산 결과가 변수 area보다 크면, area에 방금 구한 결과를 대입했다.
'코딩테스트 연습 > 투 포인터, 그리디, DP' 카테고리의 다른 글
| 다음 순열(Next Permutation) 구하기 (0) | 2023.03.01 |
|---|---|
| LeetCode 202번 - Happy Number (0) | 2023.02.02 |
| LeetCode 121번 - Best Time to Buy and Sell Stock (0) | 2023.01.28 |

